Cantrips are an integral part of The Epic Storm. They serve two main purposes: sculpting hands and searching for specific cards. If you want to read more about sculpting hands, AJ Kerrigan has a great article here. In this article, we are going to focus more on finding specific cards. The need to find specific cards quickly happens in a couple of cases: on the combo turn or early in the game in matchup such as the mirror or vs Moon Stompy.

Deck List

In v4.7, there are a total of 10 cantrips (4 Ponder, 2 Preordain, and 4 Brainstorm) and 10 win conditions (4 Infernal Tutor, 4 Burning Wish, 1 Ad Nauseam and 1 Empty the Warrens), which provides the input for all of the math for today.

on the play vs Mono Red Stompy:

Let’s look at a couple of lines, based on the idea that we want to go off this turn.

We could just start by casting Ponder looking for any Burning Wish, any Infernal Tutor, Ad Nauseam or Empty the Warrens. Empty can be risky against Stompy because of Fiery Confluence, but a turn one Empty does win a good percentage of the time. This leaves us with 10 outs in the deck to attempt to win the game. Using the calculator provided, this gives about a 57% chance to win the game. The formula looks like this:

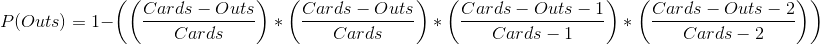
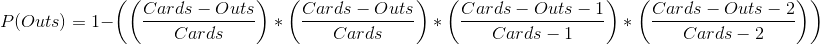
Where Outs is the number of outs in your library and Cards is the number of cards left in your library. The formula looks like this because it is calculating the probability of not missing. The formula is of the form 1 – P(Miss), or it calculates the odds of finding no outs or cantrips and then subtracts it from 1. This finds the odds of not missing, which is important to account for cases with a cantrip and an out or multiple cantrips or wins.

57% is pretty good off of just one cantrip! However in the 43% chance the Ponder does not find one of our outs, it finds another cantrip some percentage of the time. The odds to find a cantrip and not a win condition is about 27%. This probability does not account for whether the next cantrip is found in the top three or is found off of the shuffle. (That math gets hard due to having to consider all of the possible worlds and the calculator takes care of that when it goes through its procedure). Let’s take a look at what happens if we find another cantrip in the top three. Should we shuffle to try to find a win directly or failing that, shuffle into a second cantrip? Let’s take a look at the math!

To find the out, we have odds of 10/53, or about 19% to find the out. If we take the cantrip in our top three, we have odds of 10/51, about 20% and if it is a Ponder, 10/51 + 10/53 or 38% chance to find the out. If you shuffle into another cantrip (9/53 or 17% (assuming 3 Ponder, 4 Brainstorm and 2 Preordain left in the library)), that cantrip has a much better chance of finding the out. However, because of how probability works, the odds of success for each successive cantrip multiply together, creating lower overall probabilities. Thus, it is better to cast cantrips as they are found and not shuffle the Ponder. The overall probability of finding the out after casting two cantrips in this situation is about 69%. This line requires that the Lion’s Eye Diamond be cracked after the second cantrip in order to have red mana to cast a Burning Wish or Empty the Warrens.

Let’s imagine an even more aggressive route: the Lion’s Eye Diamond is cracked after the first cantrip! This gives four blue mana to cantrip through the deck with. Strangely enough, this does not increase the odds that much over finding the out after two cantrips, coming in at about 71%, only 2% higher with the ability to cast two cantrips! This is because as the odds of finding a cantrip are small and then are multiplied with the odds of finding an out off the cantrip, creating lower and lower influences on the overall probability.

The Bricked Ad Nauseam

Let’s examine another scenario: a bricked Ad Nauseam, where we end up with multiple sources of blue mana and multiple cantrips.

This is much different than the previous example because we don’t need to find new cantrips, which allows bottoming and shuffling sets of cards that do not contain the outs. Sequencing cantrips correctly what is needed to win the game. Essentially the goal is to make Ponder the best it can be and to avoid casting Brainstorm at all costs. Ponder gives the highest odds to find any given card because of its ability to shuffle. Casting a Brainstorm bricks the top of the library and makes all of the subsequent cantrips much worse. Instead of getting a full three looks, each cantrip only gets one or, if it’s a Ponder two looks. Casting Preordains gives the same odds at finding a cantrip as Brainstorm but it makes the next cantrip have better odds because the two cards it bottomed are no longer considered in the probability calculation.

To wrap it up, the most important guideline to follow is to try to keep the top of the library clean when searching for outs. Preordain effectively reduces the size of the library and increases the odds of the next cantrip finding an out. If you don’t have a cantrip in hand and you find another, casting that cantrip will give you higher odds than shuffling and trying to find another cantrip or a win.

Until next time, may the odds be ever in your favor!

Calculate Your Own Cantrips!